الحساسات - قياس تغيرات المقاومة بقنطرة هيوستون
قياس تغيرات المقاومة بقنطرة هيوستون :
لاستخدام الـ strain gage لقياس الإنفعالات strains بدقة , فإننا نحتاج إلي مقدره قياس التغيرات الصغيرة في المقاومة بدقة . من الدوائر الشائعة الإستخدام لقياس التغيرات الصغيرة في المقاومة قنطرة هيوستون Wheatstone , وهي تتكون من شبكة من أربعة مقاومات يتم إثارتها عن طريق جهد تيار مستمر Dc هناك أسلوبين مختلفين من التشغيل لدائرة قنطرة هيوستون هما : الأسلوب الأستاتيكي المتزن static balanced mode والأسلوب الديناميكي الغير متزن dynamic unbalanced mode يبين الشكل الأسلوب الاستاتيكي المتزن حيث R3 , R2 هما مقاومات الدقة precision resistors بينما R4 هي بوتانشيومتر الدقة precision potentiometer ( مقاومة متغيرة ) معه مقياس دقيق لعرض قيمة المقاومة , أما R1 فهي مقاومة الـ strain gage المطلوب قياس التغير بها . لكي تتزن القنطرة , يجب ضبط المقاومة المتغيرة حتي يصبح الجهد بين العقدتين B , A يساوي صفر . في حالة الإتزان .
ف‘إن الجهود B , A يجب أن تخضع للعلاقة :
i1 = i2R2 (8.14)
بفرض أن الفولتميتر ذو معاوقة دخل عالية الموصل بين B , A يسحب تياراً , إذن :
حيث Vex جهد التيار المستمر DC المسلط علي القنطرة ويطلق عليه جهد الإثارة excitation voltage بالتعويض بهذه التعبيرات في معادلة (8.14) وإعادة الترتيب إذن :
إذا علمنا قيم R3 , R2 بدقة ولاحظنا قيمة R4 يمكننا حساب المقاومة الغير معروفة R1 بدقة , أي أن :
لاحظ أن هذه النتيجة لا تتوقف علي جهد الإثارة Vex .
يمكن استخدام تشغيل الأسلوب الاستاتيكي المتزن لقياس مقاومة الـ gage تحت التحميل , ولكن عادة يتم الإتزان كخطوة أولية لقياس تغيرات مقاومة الـ gage في تشغيل الـ dynamic deflection مع R1 ممثلة للـ R2 , strain gage ممثلة للبوتانشيومتر , فإنه يتم عمل اتزان للقنطرة اولاً بضبط R2 حتي يصبح جهد الخرج مساوياً للصفر , ثم بعد ذلك تتغير مقاومة الـ strain gage نتيجة حدوث تحميل , ويمكن , حساب هذا التغير عن طريق تغيرات جهد الخرج .
يمكن التعبير عن جهد الخرج بدلالة تيارات المقاومة كما يلي :
V0 = i1 R1 – i2R2 = –i1R4 + i2 R3 (8.19)
ويكون جهد الإثارة :
Vex = i1 (R1 + R4) = i2(R2 + R3) (8.20)
بحساب i1 و i2 بدلالة Vex من المعادلة (8.20) وبالتعويض في المعادلة (8.19) إذن :
عندما تتزن القنطرة فإن V0 يساوي صفر ويكون لـ R1 قيمة معلومة . عندما تتغير R1 بمجرد تحميل الـ strain gage , يمكن استخدام المعادلة (8.20) لربط تغير الجهد ΔV0 بعلاقة مع التغير في المقاومة ΔR1 لإيجاد العلاقة , يمكننا إحلال R1 بالقيمة الجديدة ΔR1 V0, R1 + بالانحراف في الجهد ΔV0 إذن معادلة (8.21) تعطي :
باعادة ترتيب هذه المعادلة نحصل علي العلاقة المطلوبة بين التغير في المقاومة وجهد الخرج المقاس , إذن :
مقياس التغير في جهد الخرج ΔV0 يمكننا حساب تغير مقاومة الـ (ΔR1) gage من المعادلة 8.23 ويمكن حساب الـ strain gage من المعادلة (8.13) . يبين الشكل تأثير أسلاك التوصيل عند استخدام strain gage موضوعة بعيداً عن دائرة القنطرة . بهذا التوصيف , تضاف مقاومات كل سلكه توصيل R' الي مقاومة فرع الـ strain gage بالقنطرة . المشكلة في هذا أنه إذا تغيرت درجة حرارة السلك , فإن هذا يسبب تغير مقاومة فرع القنطرة , يمكن أن يكون هذا التأثير جوهري إذا كان السلك , فإن هذا يسبب تغير في مقاومة فرع القنطرة . يمكن أن يكون هذا التأثير جوهري إذا كان السلك طويل ويمتد عبر بيئات قد تتغير فيها درجة الحرارة . يبين الشكل وصلة من ثلاث أسلاك لحل هذه المشكلة . بهذا التوصيف , تضاف مقاومة متساوية للأسلاك إلي الأفرع المتجاورة في القنطرة بذلك تلغي التأثيرات تغيرات المقاومة بعضها البعض . يوصل السلك الثالث بدائرة قياس جهد معاوقة الدخل العالية ولا تأثير لمقاومته يذكر حيث فيها تيار مهمل . عادة تكون الأسلاك الثلاثة تكون في شكل كابل شريطي ribbon cable صغير لكي نتأكد أن الثلاثة تكون تغيرات الحرارة فيهم متساوية وكذلك لتقليل التداخل الكهرومغناطيسي الناتج من الربط التأثيري .
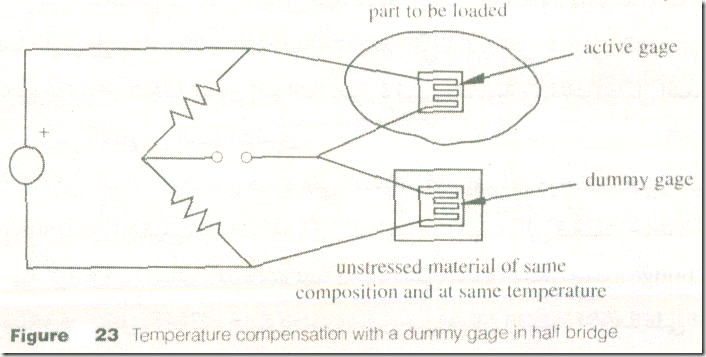
بالإضافة إلي تأثيرات درجات الحرارة علي الأسلاك , فإن تغيرات درجات الحرارة في الـ strain gage يمكن أن تسبب تغيرات كبيرة في المقاومة مما يؤدي إلي قياسات خاطئة هناك وسلة سهلة لإزالة هذا التأثير , تستخدم فيها دائرة يطلق عليها النصف قنطرة half bridge وهي موضحة في الشكل حيث يحتوي ساقين من سيقان القنطرة الأربعة علي أثنين strain gage الـ strain gage بالفرع العلوي هي الـ gage الفعالة المستخدمة لقياس انفعالات السطح للعنصر المعرض للتحميل أما الـ gage الثانية فهي دمية dummy يتم تركيبها علي عينة من مادة مطابقة لمادة العنصر . إذا تم الحفاظ علي درجة حرارة العينة بحيث تكون مساوية .
لدرجة حرارة العنصر وذلك يجعلهم قريبين من بعضهم , إذن فإن تغيرات المقاومة في الاثنين gages نتيجة يلغي بعضها البعض لأنها في فرعين متجاورين بالقنطرة لذلك فإن القنطرة تولد جهد غير متزن فقط استجابة للـ strain الذي في الـ active gage .







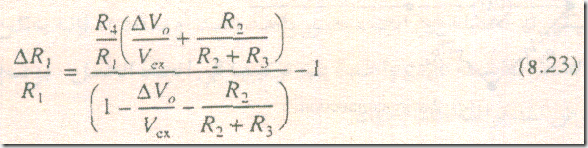



تعليقات
إرسال تعليق