الحساسات - قياس حالات مختلفة للإجهاد بالـ strain gages
قياس حالات مختلفة للإجهاد بالـ strain gages :
ممكن أن تأخذ العناصر الميكانيكية أشكالاً مركبة وغالبا ما تتعرض لظروف تحميل مركبة . في مثل هذه الحالات , يكون من الصعب التنبؤ بموضع الاجتهادات الأساسية عند نقط اختيارية علي العنصر . ومع ذلك , ببعض الهندسيات وظروف التحميل يمكن معرفة المحاور الأساسية ويكون قياس حالة الإجهاد أسهل .
إذا فرضنا عنصر ميكانيكي تم تحميله في إتجاه محور واحد ( شد أو ضغط ) , فإنه يمكن تعيين حالة الإجهاد في العنصر بواسطة gage واحدة يتم تركيبها في اتجاه الحمل , يوضح الشكل قضيب يتعرض لشد يرافقه حالة إجهاد .
بقياس الانفعال Ex , فإنه يمكن حساب الإجهاد باستخدام قانون هوك , إذن :
σ= Eεx (8.24)
where the axial stress in the bar σx is given by
حيث A مساحة مقطع القضيب . بالتالي , يمكن حساب القوة p المسلطة علي القضيب من قياس الـ strain gage , إذن :
P = AEεx
بفرض أن لدينا عنصر ميكانيكي معروف أنه تعرض لحمل ثنائي المحورية ( أي الحمل في اتجاهين متعامدين , شد أو ضغط ) فإن حالة الإجهاد بالعنصر يمكن تعيينها بواسطة اثنين strain gage كل منهما في اتجاه إجهاد من الإثنين يبين الشكل خزان يتعرض لضغط يقترن به حالة إجهاد . بقياس الانفعال Ex , فإن الاجتهادات في الخزان يمكن حسابها عن طريق قانون هوك للإتجاهين y , x إذن :
εx = σx/E - V σx/E (9.27)
εy = σy/E - V σx/E (9.28)
بحل المعادلتين السابقتين نحصل علي مركبتي الإجهاد , إذن :
Solving for the stress components gives
حيث p الضغط الداخلي , t سمك جدار الخزان , r نصف قطر الخزان xσ هو الإجهاد العرضي ويطلق عليه loop stress , بينما σy هو الإجهاد الطولي ويطلق عليه axial stress . يمكن استخدام المعادلة (8.29) أو المعادلة (8.30) لحساب الضغط في الوعاء vessel (الخزان) علي أساس قياسات الـ strain gage طبقاً :
أي من المعادلتين تعطي قيمة الضغط الصحيح لوعاء جدارة رفيع بدون خطأ في القياسات .
في هذا المثال تخدم ال strain gage كمحول طاقة للضغط pressure tranducer .
بالنسبة للتحميل الأحادي المحور uniaxial والتحميل الثنائي المحور biaxial , فإننا نعلم أثنين gages (واحدة لأحادي المحور بينما اثنين لثنائي المحور ) لتعيين قيم الاجهادات .
ومع ذلك , في حالة التحميل المركب أو في حالة أن تكون هندسية العنصر الميكانيكي أكثر تعقيداً فإن التصميم الميكانيكي يحتاج تركيب ثلاثة gages strain بالاسم strain gage rosette . هناك نوعيات كثيرة من الـ rosettes المتاحة تجارياً مع اثنين أو أكثر من الـ grid patterns موضحة بدقة علي عبوة (تغليف) واحدة بتقاربية عالية close proximity , أنظر الشكل .
أكثر الـ rosette patterns شيوعاُ° هي المستخدمة لقياس الحالة العامة للإجهاد planar stress وهي الموضحة في الشكل , حيث تبدو الـ grids كخطوط فردية معنوية بالحروف . أكثر هؤلاء شيوعاً الـ strain gage المستطيلة , حيث تبعد الـ strain gage عن بعضها بزاوية مقدارها 45° ( أنظر الشكل ) . يبين الشكل عدة rosettes ثلاثية الـ gages المتاحة تجارياً .
باستخدام مبادئ ميكانيكا الأجسام الصلبة , فإنه يمكن حساب قيمة واتجاه الاجهادات الأساسية مباشرة من قياسات الانفعال اللحظية عن طريق rosette patterns الموضحة في الشكل . قيمة واتجاه الاجهادات الأساسية principal stresses للـ rosette المستطيل هي :
حيث Eb , Ea انفعالات كل من الـ rosette gages , θp هي الزاوية من الـ (a) gage إلي اتجاه أقصي إجهاد أساسي ويمكن حساب θp عن طريق المعادلة (8.36) بتعيين الزاوية المقابلة للـ tan . إذا كان البسط موجب
(εb > εa + εc)/2)
فإن 2θp تقع في الربع الأول أو الربع الثاني لذلك فإن
0 < θp < 90 °
. خلاف هذا , وقوع 2 θp في الربع الثالث أو الربع الرابع فإن .
-90 ° < θp < 90 °
اإذا كان البسط في المعادلة (8.39) موجب (Ec > Eb ) فإن 2θp تقع في الربع الأول أو الثاني بذلك فإن
0 < θp < 90 °
. خلاف هذا , فإن
2 θp
تقع في الربع الثالث أو الرابع فيكون .
0 < θp < 90 ° .
العلاقات للـ t-delta rosette التي بها أربعة : gages in
إذا كان البسط في المعادلة (8.42) موجب (Ec > Eb ), فإن 2θp تقع في الربع الأول أو الربع الثاني لذلك فإن
0 < θp < 90 ° .
خلاف هذا , فإن 2θp تقع في الربع الثالث أو الرابع بذلك فإن
. -90 ° < θp < 0 .






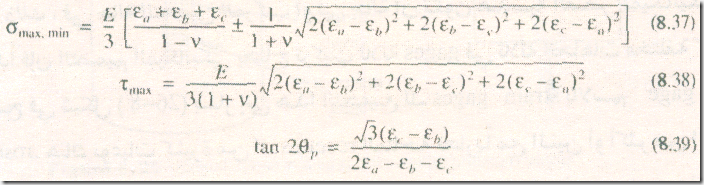





تعليقات
إرسال تعليق