الحساسات : قياس الاهتزاز والعجلة Vibration and Acceleration Measurement
قياس الاهتزاز والعجلة :
Vibration and Acceleration Measurement
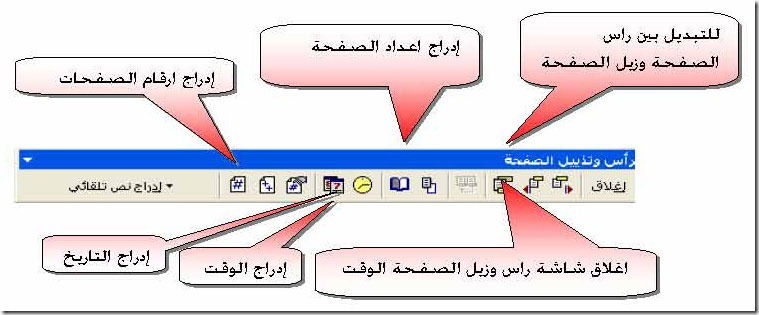
الـ accelerometer هو حساس صمم لقياس الاهتزاز الميكانيكي المستمر مثل اهتزاز كراسي المحور bearning والارتعاش في الديناميكا الهوائية والاهتزازات العابرة مثل الموجات الصادمة ومثل هبات الرياح أو التصادمات . الـ accelerometers عادة تكون موصلة ميكانيكيا أو مربوطة بالجسم أو البناء المراد قياس العجلة له . يكشف جهاز قياس العجلة accelerometer''" عن العجلة علي طول محور واحد وهو حساس للحركة في الاتجاة العمودي . تحتوي الـ strain gages والعناصر الكهروضغطية piezoelectricعلي عنصر استشعار جهاز قياس العجلة , يقوم بتحويل الإهتزاز إلي إشارة جهد . يتأسس تصميم الـ accelerometer علي التأثيرات الداخلية المرافقة لكتلة الموصلة بالجسم المتحرك من خلال يأي وكابت damper وحساس إزاحة displacement sensor . يوضح الشكل accelerometer بمرجعية إزاحة displacement reference معه مخطط الكتلة والقوي المؤثرة عليها . عندما يتعرض الجسم لعجلة فإنه ستكون هناك حركة نسبية بين الـ housing والكتلة المعرضة للإهتزاز seismic mass . يستشعر محول قدرة الإزاحة هذه الحركة النسبية . من خلال تحليل الاستجابة الترددية للتمثيل الرياضي modelling لنظام المرتبة الثانية للـ accelerometer , فإنه يمكننا ربط إزاحة خرج الـ transducer إما بالموضع المطلق أو بعجلة الجسم . لتعيين الاستجابة الترددية frequency response للـ accelerometer , نقوم اولاً بالتعبير عن القوة الموضحة في مخطط الكتلة . لنفعل هذا , فإننا نقوم بتعريف الإزاحة النسبية x بين الكتلة والجسم , إذن :
Xr = xo – xi (8.52)
تم قياس هذه الإزاحة عن طريق محول طاقة الموضع position transducer الموجود بين الكتلة والـ housing . إذن يمكن التعبير عن قوة اليأي :
Fx = K(x0 – xi ) = kxr (8.53)
ويمكن التعبير عن قوة الكابت كما يلي :
الحروف المنقوطة تمثل التفاضلات الزمنية . بتطبيق قانون نيوتن الثاني فإن معادلة الحركة للكتلة تكون :
أخذت القوي إشارات سالبة في المعادلة لأنها في إتجاه مضاد للإتجاه المرجعي X0 .
بالتعويض في المعادلة (8.53) والمعادلة 8.54 , إذن :
حيث الإزاحة النسبية X2 هي :
يمكن استبدال X0 بـ :
وبالتالي كتابة المعادلة (8.57) بالشكل :
والتي يمكن إعادة صياغتها علي الصورة :
تربط هذه المعادلة التفاضلية التي من الرتبة الثانية بين الإزاحة النسبية المقاسة Xr وإزاحة الدخل Xi . وكما درسنا سابقا في تحليل نظام الرتبة الثانية , فإنه يمكننا إعادة صياغة هذه المعادلة إلي الصورة
حيث التردد الطبيعي :
ونسبة الكبت :
لتعيين الإستجابة الترددية , نفرض أن إزاحة الدخل تكون في صورة جيبيه ولتكن :
ولأن النظام خطي , فإن الإزاحة النسبية الناتجة للخرج تكون أيضاً جيبيه بنفس التردد ولكن مع إختلاف في الطور :
إذن تحليل الاستجابة الترددية كنسبة للقيمة يكون :
للربط بين إشارة إزاحة الخرج النسبية Xr وعجلة الدخل Xi , نقوم بتفاضل المعادلة (8.65) , إذن :
حيث قيمة دخل العجلة هو :
X1w2
إعادة صياغة المعادلة (8.67) إذن :
حيث (ω)Ha أستخدمت لتمثيل النسبة (Xr ω2n)/(Xi ω2) كدالة في التردد ω . توضح الأشكال العلاقة بين هذا الحد وزاوية الطور بيانياً عند قيم مختلفة لنسبة الكبت damping ratio مقام Ha(ω) هو قيمة عجلة الدخل Xi ω2 , بينما البسط هو ضرب قيمة إزاحة الخرج Xr ومربع التردد الطبيعي natural frequency (ω2n) . إذن يمكننا الربط بين قيمة إزاحة الخرج المقاسة بقيمة عجلة الدخل أي أن :
إذن يمكن التعبير عن قيمة عجلة الدخل كما يلي :
إذا كنا نصمم accelerometer لكي تكون Ha(ω) قريبة من 1 خلال مدي ترددي كبير , إذن تكون قيمة عجلة الدخل دالة مباشرة في قيمة الإزاحة النسبية مضروبة في معامل ثابت ω2n :
وكما هو موضح في الشكل أن أكبر مدي ترددي ناتج بنسبة قيمة قدرها الوحدة يحدث عند نسبة كبت قدرها -0.707 وتكون ωn التردد الطبيعي كبيرة بأقصي قدر ممكن . أيضاً , كما هو واضح في الشكل أنه عندما تكون مساوية للقيمة 0.707 فإنها تنتج أفضل خطية طور للنظام . يمكننا جعل التردد الطبيعي ωn كبيراً عن طريق اختيار كتلة اهتزازية صغيرة وثابت يأي كبير . يمكن إتمام ذلك في عبوة صغير جداً مناسبة للـ accelerometers التجارية . تطبيق المعادلة (8.74) علي كل مركبة ترددية ω تقع داخل نطاق تردد الحساس . إذا كان لدينا دخل إختياري يتكون من عدد من الترددات التي تقع داخل نطاق التردد , كل تردد يساهم في الإشارة الممثلة بالمعادلة (8.74) وكانت العجلة تتناسب مع الإزاحة النسبية الكلية المقاسة , إذن :
نفس توصيف الـ spring – mass – damper المستخدم لقياس العجلة يمكن تصميمه لقياس الإزاحة بدلاً من العجلة . هذا من الأجهزة يطلق عليه Vibrometer . إن نسبة القيمة amplitude ration المعطاة في المعادلة (8.67) تقدم لنا العلاقة الضرورية بين الدخل وإزاحات الخرج . فكما فعلنا في تحليل الـ accelerometer يمكننا الأن تعريف نسبة الإزاحة كما يلي :
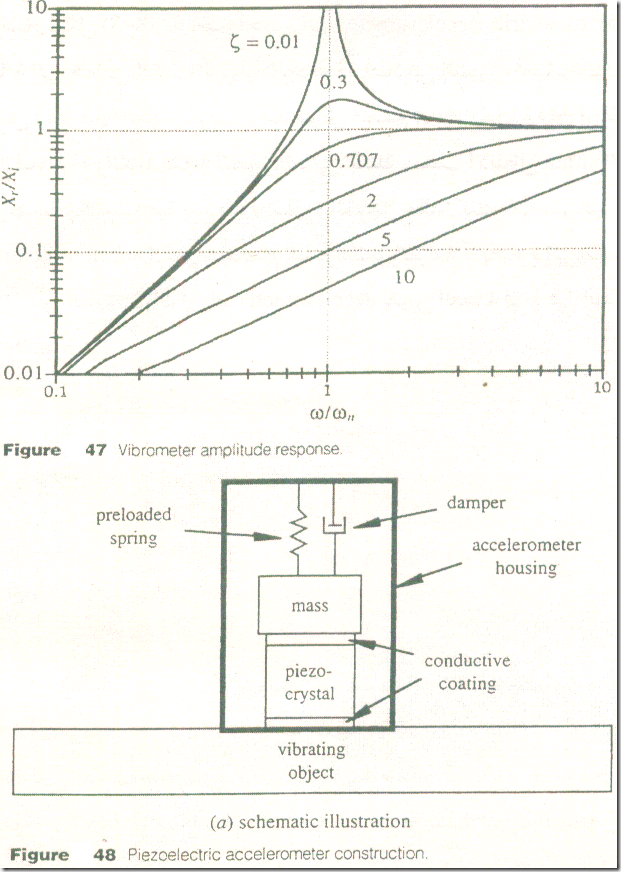
يوضح الشكل العلاقة بين نسبة القيمة والتردد لقيم مختلفة لنسبة الكبت damping ratio علاقة زاوية الطور phase angle مماثلة للـ accelerometer (أنظر الشكل ) هناك علاقة بين قيمة إزاحة الدخل Xi وقيمة الإزاحة النسبية المقاسة هي :
إذا صممنا الـ Vibrometer لكي تكون Ha(ω) قريبة من الواحد خلال مدي تردد كبير إذن فإن قيمة إزاحة الدخل تعطي مباشرة عن طريق قيمة الإزاحة النسبية , أي أن :
فكما يمكننا أن نري من الشكل , فإن أكبر مدي تردد ينتج مع نسبة قيمة مقدارها الوحدة وتحدث عند كبت قدرها 0.707 وتردد طبيعي ωn صغير بقدر الإمكان . يمكننا جعل التردد الطبيعي صغير عن طريق اختيار كتلة إهتزازية كبيرة وثابت بأي صغير . هذا يفسر كبر حجم الـ seismographs المستخدم لقياس الحركة نتيجة الزلازل .

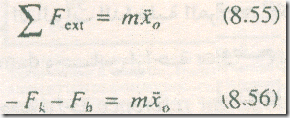


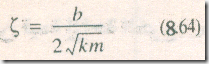










تعليقات
إرسال تعليق